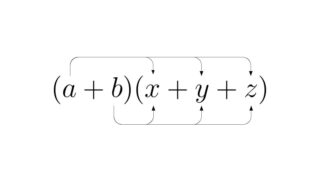多項式 多項式の計算Ⅰ（加法・減法・乗法）
いくつかの多項式の和・差・積の形で表された式は，交換法則，結合法則，分配法則を繰り返し用いることで\(\,\)1\(\,\)つの多項式に変形することができます。1．数と多項式の積多項式どうしの計算の前に，数と多項式の乗法に触れておきます。例...
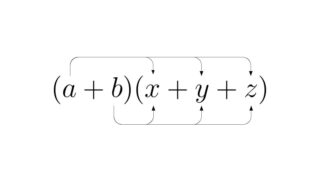多項式 
多項式 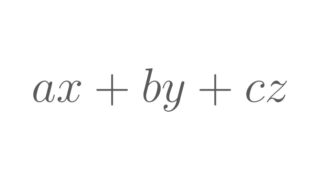多項式の基礎事項
数学では文字を含む式をよく扱います。その中で最も基本的なのは，多項式と呼ばれる式で，\(6xy\)，\(2a+4\)，\(x^2-x+1\) のように，数と文字とが乗法と加法で結びついている式です。多項式は学習の各段階で現れます。その計算が...
数学 倍数の判定法（7，11の倍数）
\(11\) の倍数の判定\(11\) の倍数の判定法は，次のものが知られています。(偶数桁目の数の和) と (奇数桁目の数の和) の差が \(11\) の倍数\(\quad \cdots\cdots \quadⒶ\)例 \(1\)\(47...
数学 倍数の判定法（2，3，5など）
1．倍数と約数2 つの整数 \(a,\;b\) について，整数 \(k\) を用いて \(a=bk\) と表されるとき，\(b\) は \(a\) の約数であるといい，\(a\) は \(b\) の倍数であるといいます。例えば，\(6=2\...
図形と方程式 領域と最大・最小～線形計画法
領域とは1．定義と簡単な例変数 \(x,\,y\) についての不等式を満たす座標平明上の点 \(x,\,y\) 全体の集合を，その不等式の表す領域といいます。いくつかの例を見てみましょう。例 1 不等式 \(y>-x+1\;\cdots\...
図形と方程式 2直線の交点を通る直線
方程式\(\;y-y_1=m(x-x_1)\;\cdots\cdots\;①\;\)は，点\(\;(x_1,\,y_1)\;\)を通り，傾きが\(\;m\;\)の直線を表す。いうまでもなく，点\(\;(x_1,\,y_1)\;\)は 2 直...
図形と方程式 円の接線の方程式
準備直線の方程式異なる 2 点 \((x_1,y_1)\)，\((x_2,y_2)\) を通る直線の方程式を，単に \ としてはいけない。\(x_1=x_2\) のときは 0 で割ることになるからである。したがって，次のように場合分けが必要...
波 自由端反射・固定端反射の反射波の作図
§1．反射について媒質を進む波は，その媒質の端において跳ね返ります。これを反射といい，反射する前の波を入射波，反射によって現れる波を反射波といいます。媒質の端には，次の 2 種類があります。自由に動くことのできる端（自由端）固定された端（固...
場合の数と確率 重複組合せの考え方
§1．はじめに異なるものの順列や組合せ，重複順列に比べると，重複組合せは難しいと考える人もいるのではないでしょうか。異なる \(n\) 個のものから重複を許して \(r\) 個取る組合せの総数は，次の式で表されます。 \ 教科書などでは，こ...