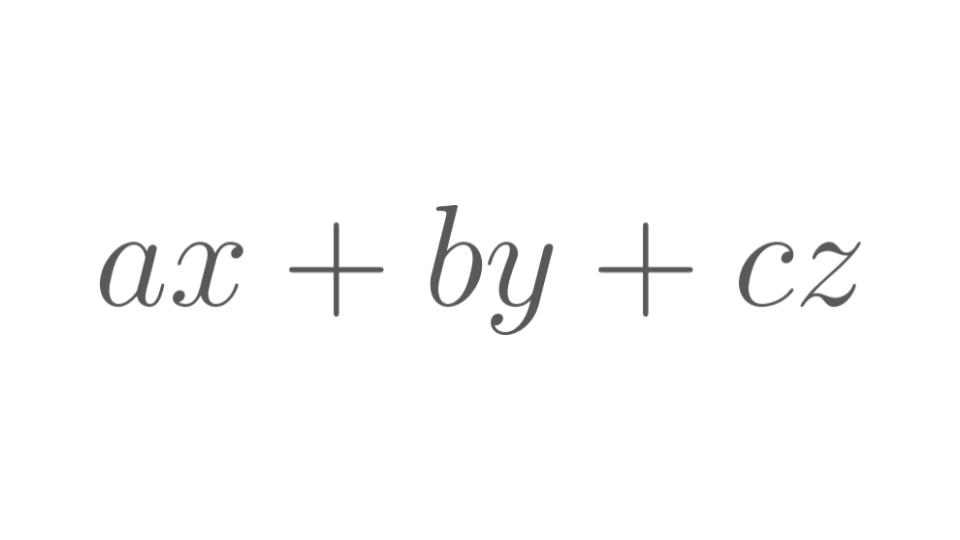多項式の基礎事項
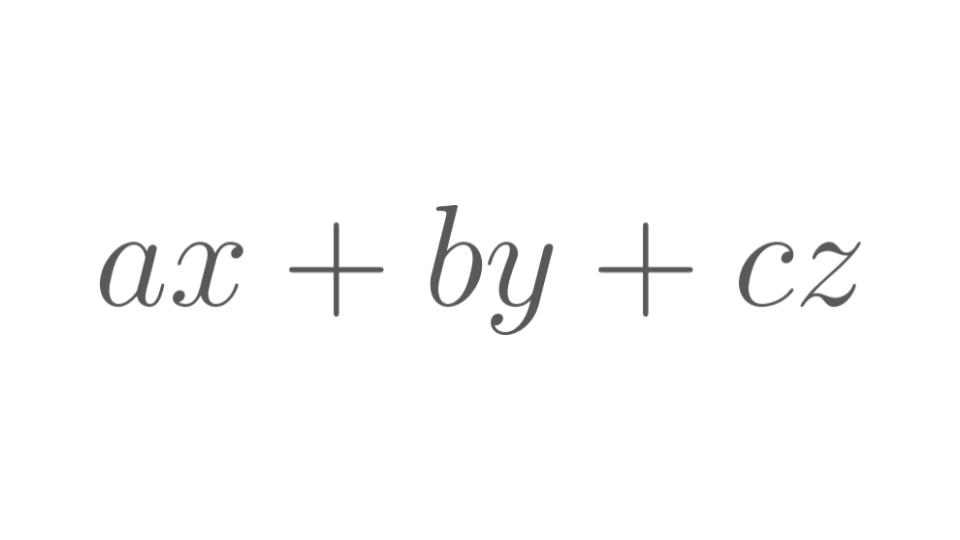 多項式
多項式
数学では文字を含む式をよく扱います。その中で最も基本的なのは,多項式と呼ばれる式で,\(6xy\),\(2a+4\),\(x^2-x+1\) のように,数と文字とが乗法と加法で結びついている式です。
多項式は学習の各段階で現れます。その計算がおぼつかないせいで学習に支障をきたすことがないよう,はじめに計算を十分に習得しておく必要があります。
1.単項式
数や文字,またそれらを掛け合わせて得られる式を単項式といいます。次に挙げる式はすべて単項式です。
例 \(1\)
\[-5a,\;9,\;xy^2,\;b,\;\frac{\;4\;}{7}x^2\]
いずれも数や文字,あるいはそれらを掛け合わせてできています。
一方で,\(\displaystyle \frac{\;1\;}{x}\) は単項式ではありません。数や文字ではなく,また数や文字をどのように掛け合わせても得られないからです。
a.式の書き方
単項式の書き方について,いくつかの決まりがあります。
① 乗算記号\(\times\)は省き,数は左端に書く。
\(a \times 2 \times x\) は \(2ax\) と書きます。ただし,\(1 \times x\) や \(x \times (-1)\) などはそれぞれ \(x\),\(-x\) と書きます。
② 同じ文字の積は,累乗の表記を用いて書く。
数(あるいは文字)\(a\) を \(n\) 個掛け合わせたものを \(a\) の \(n\) 乗といい,\(a^n\) と書きます。\(a\) の右上に小さく書いた \(n\) を \(a^n\) の指数といいます。
\[a^1=a,\;\;a^2=a \times a,\;\;a^3=a \times a \times a,\;\cdots \cdots \]
であり,それぞれ \(a\) の \(1\) 乗,\(a\) の \(2\) 乗,\(a\) の \(3\) 乗,\(\cdots \cdots\) です。総称して \(a\) の累乗といいます。
この表記を用いると,\(abbccc\) は \(ab^2c^3\) と表すことができます。
文字はアルファベット順に書くことが多いですが,絶対的なルールではありません。\(3ka\) のように書くこともあります。
b.係数と次数
単項式において,数の部分を係数といい,掛け合わされている文字の個数を次数といいます。\(0\) 以外の数だけからなる単項式の次数は \(0\) とし,数 \(0\) の次数は定めません。
例題 \(1\)
例 \(1\) で挙げた各単項式について,その係数と次数を述べよ。
解答
解答
| 係数 | 次数 |
| \(-5a\) | \(-5\) | \(1\) |
| \(9\) | \(9\) | \(0\) |
| \(xy^2\) | \(1\) | \(3\) |
| \(b\) | \(1\) | \(1\) |
| \(\displaystyle \frac{\;4\;}{7}x^2\) | \(\displaystyle \frac{\;4\;}{7}\) | \(2\) |
2.多項式
a.多項式の定義
いくつかの単項式が加法や減法で結びついた式を多項式といいます。
例 \(2\)
\[x^3-3x+1,\;\;2n+3,\;\;a^2-b+2c-5,\;\;3xy+4z^2+2\]
多項式は単項式の和の形に書き表すことができる式ともいえます。
例 \(2\) では \(1\) つ目の多項式と \(3\) つ目の多項式がそれぞれ
\[\begin{align}
&x^3-3x+1=x^3+(-3x)+1\\\\
&a^2-b+2c-5=a^2+(-b)+2c+(-5)
\end{align}\]
と表すことができます。
多項式を単項式の和の形で表したとき,各単項式をその多項式の項といい,特に文字を含まない数だけの項は定数項とよばれます。
例題 \(2\)
例 \(2\) で挙げた各多項式の定数項を述べよ。
解答
定数項の定義にしたがって答えます。
解答
順に \(1,\;\;3,\;\;-5,\;\;2\)
b.計算規則,式の整理
多項式の計算も,数と同様に交換法則,結合法則,分配法則を基礎としておこなわれます。
多項式の計算
\(A,\;B,\;C\) は多項式とする。
\(A+B=B+A, \quad AB=BA\)
\((A+B)+C=A+(B+C),\quad (AB)C=A(BC)\)
\(A(B+C)=AB+AC,\quad (A+B)C=AC+BC\)
\(1\) つの多項式のなかで,文字の部分が一致する項を同類項といいます。同類項は分配法則を用いて,例えば次のように \(1\) つにまとめられます。
\[\begin{align}
\frac{\;4\;}{3}ax^2+\frac{\;5\;}{2}ax-2ax+ax^2&=\Big(\frac{\;4\;}{3}+1\Big)ax^2+\Big(\frac{\;5\;}{2}-2\Big)ax\\\\
&=\frac{\;7\;}{3}ax^2+\frac{\;1\;}{2}ax
\end{align}\]
このように同類項をまとめることを,多項式を整理するといいます。
\(ax^2\) と \(ax\) は文字の種類は同じでも掛け合わされた個数が違うので,\(\displaystyle \frac{\;7\;}{3}ax^2\) と \(\displaystyle \frac{\;1\;}{2}ax\) は同類項ではなく,さらにまとめることはできません。
多項式を整理して残った項のうち,最高次数の項の次数を,その多項式の次数といい,次数が \(n\) の多項式を \(n\) 次式といいます。
例題 \(3\)
次の多項式は何次式であるか答えよ。
\((1)\;\;3x-4+4x^2+1-x^2+2x\)
\((2)\;\;3y^2-8+y^2+2y-3-4y^2+2y\)
\((3)\;\;6ab-b+2a^2b-3+3ab\)
解答
解答
\(3x-4+4x^2+1-x^2+2x=3x^2+5x-3\qquad\)
よって,\(2\) 次式
\(3y^2-8+y^2+2y-3-4y^2+2y=4y-11\qquad\)
よって,\(1\) 次式
\(6ab-b+2a^2b-3+3ab=2a^2b+9ab-b-3\qquad\)
よって,\(3\) 次式
多項式の次数は,式を整理してから考えます。\((2)\) では \(2\) 次の項がありますが,整理すると消えるので,間違えないように注意が必要です。
さて,せっかく登場した「単項式」という用語ですが,今後目にする機会はほぼないかと思います。というのは,単項式を「項が \(1\) つの多項式」と考えて,多項式のうちに含めるのがふつうだからです。以降,「多項式」という語は,単項式を含むものとして使用します。
また,この意味での「多項式」と同じ意味で,整式という言葉が使われることもあります。
c.一部の文字に着目する
\(1\) つの多項式のなかに複数の種類の文字が含まれるとき,その一部の文字に着目して考えることがあります。このとき,着目した文字だけを文字と考え,その他の文字は数として扱います。
同じ多項式でも,着目する文字によって次数や定数項などは変わってきます。
例題 \(4\)
\(\quad(1)\quad\)\(3a^3bc^2\) について,\(a\) に着目したときの係数と次数を述べよ。また,\(b\) と \(c\) に着目した場合はどうか。
\(\quad(2)\quad 2ax^2-3xy+by^2-4abx+5by+6a-7\) について,\(x\) と \(y\) に着目したときの次数と定数項を述べよ。
\(\quad(3)\quad 2kx^2+3k^2x+4kx-x^2+10x-1\) を \(x\) に着目して整理し,次数と定数項を述べよ。また,\(k\) に着目した場合はどうか。
解答
解答
\(\quad(1)\quad\)\(a\) に着目したとき,係数は \(3bc^2\),次数は \(3\)。
\(b\) と\(c\) に着目したとき,係数は \(3a^3\),次数は \(3\)。
\(\quad(2)\quad\)次数は \(2\),定数項は \(6a-7\)。
\(\quad(3)\quad\)\(x\) について整理すると \[(2k-1)x^2+(3k^2+4k+10)x-k^2\] よって,次数は \(2\),定数項は \(-k^2\)。
\(k\) について整理すると \[(3x-1)k^2+(2x^2+4)k+(-x^2+10x)\] よって,次数は \(2\),定数項は \(-x^2+10x\)。
着目した文字以外の文字は数として扱います。
\(\quad(1)\quad\)\(a\) に着目したときは,\(b\) と \(c\) を数として扱うので,数を左端に書くと \(3bc^2 \cdot a^3\) です。よって,係数(数の部分)は \(3bc^2\)となります。また,文字として扱うのは \(a\) だけですから,掛け合わされた文字の個数,すなわち次数は \(3\) です。\(b\) と \(c\) に着目したときも同様に考えます。
\(\quad(2)\quad\)\(x\) と \(y\) は文字,\(a\) と \(b\) は数です。各項について,\(x\) と \(y\) が掛け合わされた個数を調べると,最大で \(2\) なので,この多項式の次数は \(2\) です。定数項(文字を含まない数だけの項)は,\(x\) も \(y\) も含まない項ですから,\(6a-7\) となります。
\(\quad(3)\quad\)\(x\) に着目したときは,例えば \(2kx^2\) と \(-x^2\) は同類項なので \(1\) つにまとめられます。次数や定数項の考え方は \((2)\) と同じです。\(k\) に着目したときも同様です。
例題 \(4\) の \((3)\) の多項式は,\(x\) に着目すると \(2\) 次式 です。このような場合,この多項式は \(x\) の(あるいは \(x\) についての)\(2\) 次式であるといいます。
\((2)\) の多項式は,\(x\) と \(y\) の \(2\) 次式です。
4.式の整理のしかた
多項式の項は自由に入れ替えることができます。\[\begin{align}
&①\;x^3-2x^2+5x-1\\\\
&②\;-1+5x-2x^2+x^3\\\\
&③\;-2x^2-1+5x+x^3\\\\
&④\;5x-1+x^3-2x^2
\end{align}\] などはすべて同じ多項式を表します。
とはいえ,③と④は散らかっているように見えて,式を「整理」するという表現にそぐわない項の並べ方です。
通常は,①のように次数が低くなるように並べるか,②のように次数が高くなるように並べます。
\(1\) つの文字に着目して多項式を整理するとき,次数が高い方から低い方へ項を並べる整理のしかたを降べきの順に整理するといい,次数が低い方から高い方へ項を並べる整理のしかたを昇べきの順に整理するといいます。
例題 \(5\)
多項式 \[7a^2x-3ax^3+4a^3x^2-5+ax-4x^2\] を
\(\quad(1)\quad\)\(x\) について降べきの順に整理せよ。
\(\quad(2)\quad\)\(a\) について昇べきの順に整理せよ。
解答
解答
\(\quad(1)\quad-3ax^3+(4a^3-4)x^2+(7a^2+a)x-5\)
\(\quad(2)\quad(-4x^2-5)+(-3x^3+x)a+7xa^2-4xa^3\)