§1.反射について
媒質を進む波は,その媒質の端において跳ね返ります。これを反射といい,反射する前の波を入射波,反射によって現れる波を反射波といいます。
媒質の端には,次の 2 種類があります。
- 自由に動くことのできる端(自由端)
- 固定された端(固定端)
同じ波形をもつ波が反射した場合でも,媒質の端が自由端であるか固定端であるかによって,反射のしかたが異なります。
§2.自由端反射
媒質の端が自由端であるときの反射を自由端反射といいます。
画像 a は,自由端反射の様子を示したものです。入射波を赤色の実線,反射波を青色の実線,これらの合成波を緑色の実線で表しています。
媒質の端 \(\mathrm{O}\) が自由端のとき,端における入射波による振動と反射波による振動は同位相です。
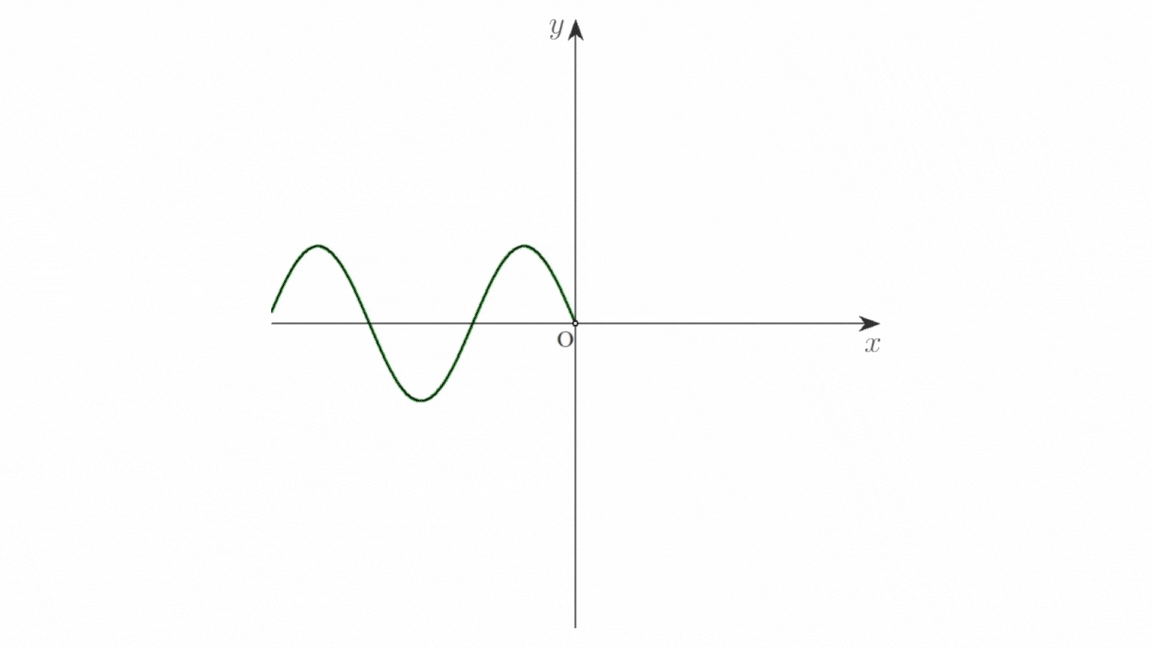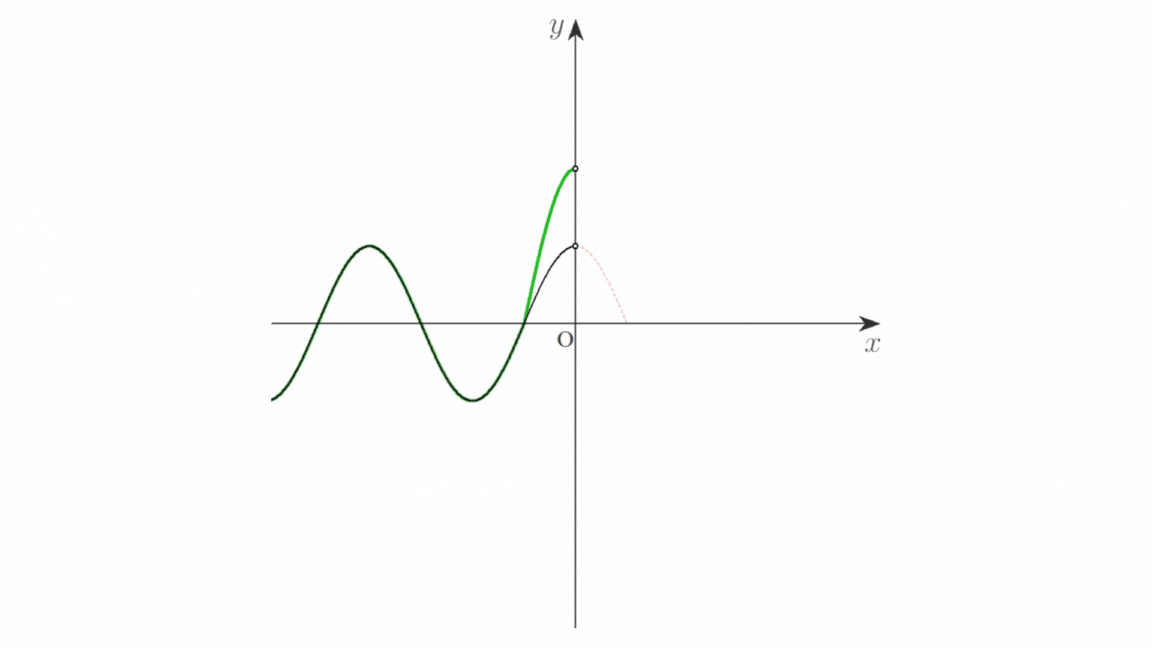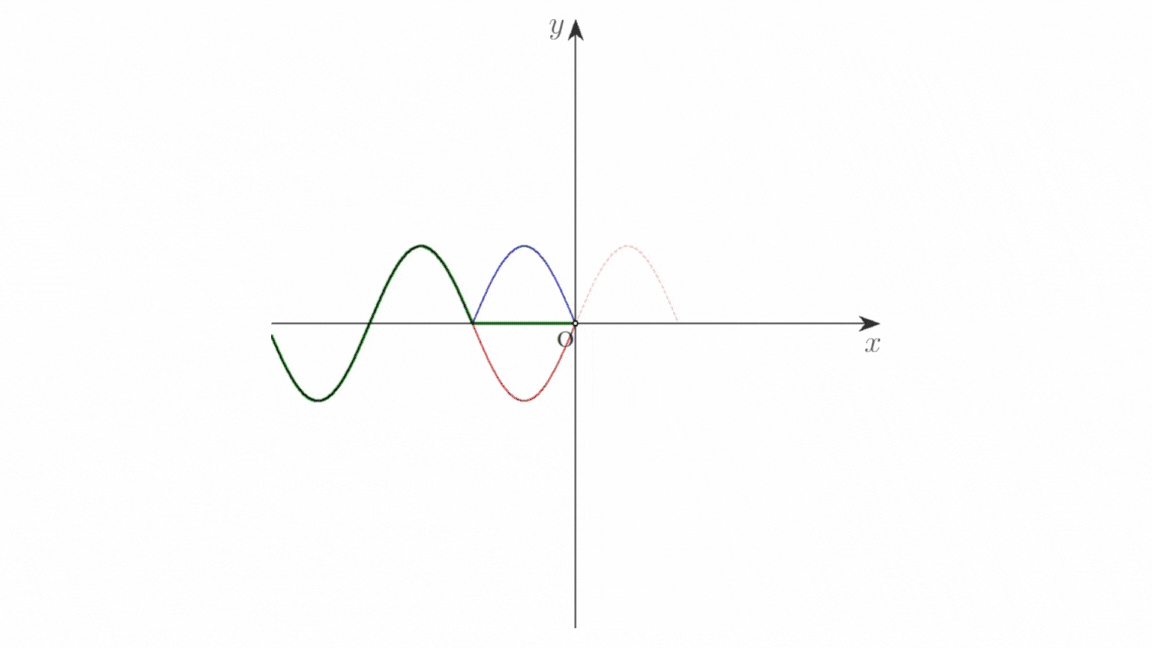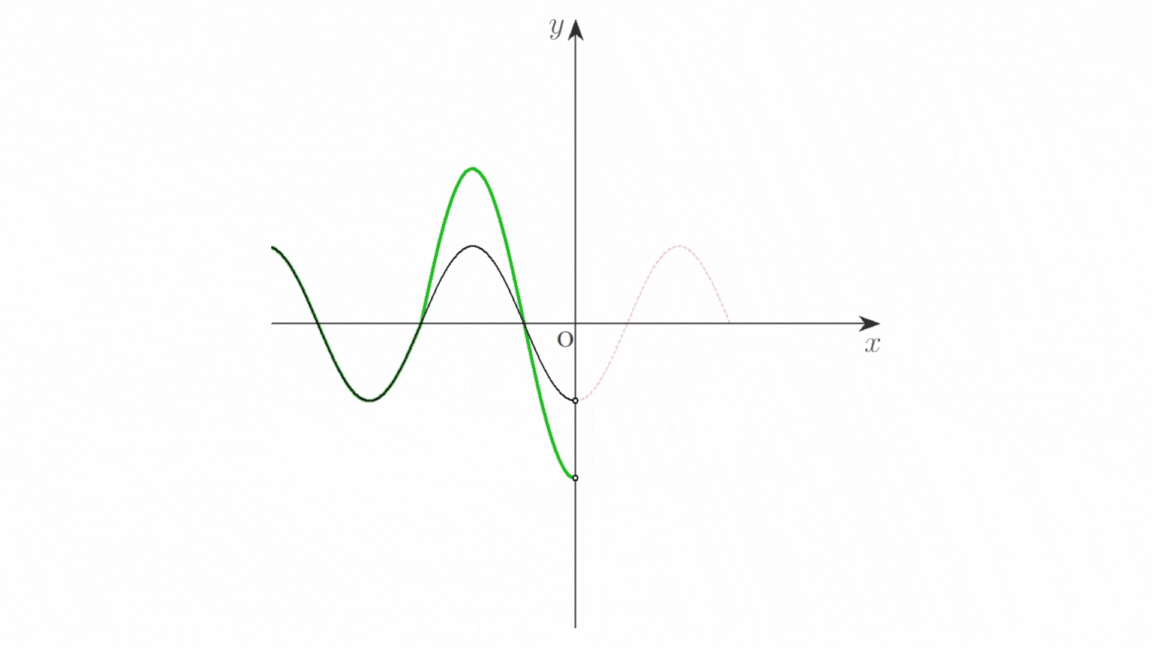
画像 a(クリックで拡大)
もし \(\mathrm{O}\) が媒質の端でないならば,\(\mathrm{O}\) の振動は \(x\) 軸の正の向きに伝わり,赤色の破線で示した波が生じます。この波がはね返るので,反射波の波形は赤色の破線を \(y\) 軸に対して折り返した青色の実線で表されます。
§3.固定端反射
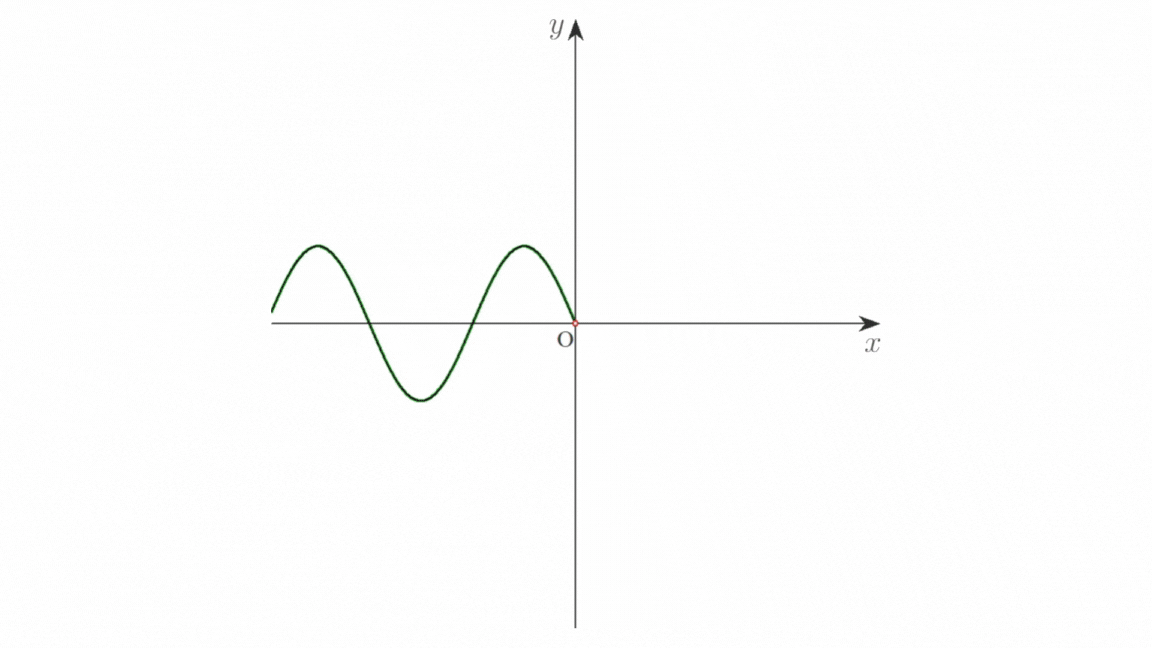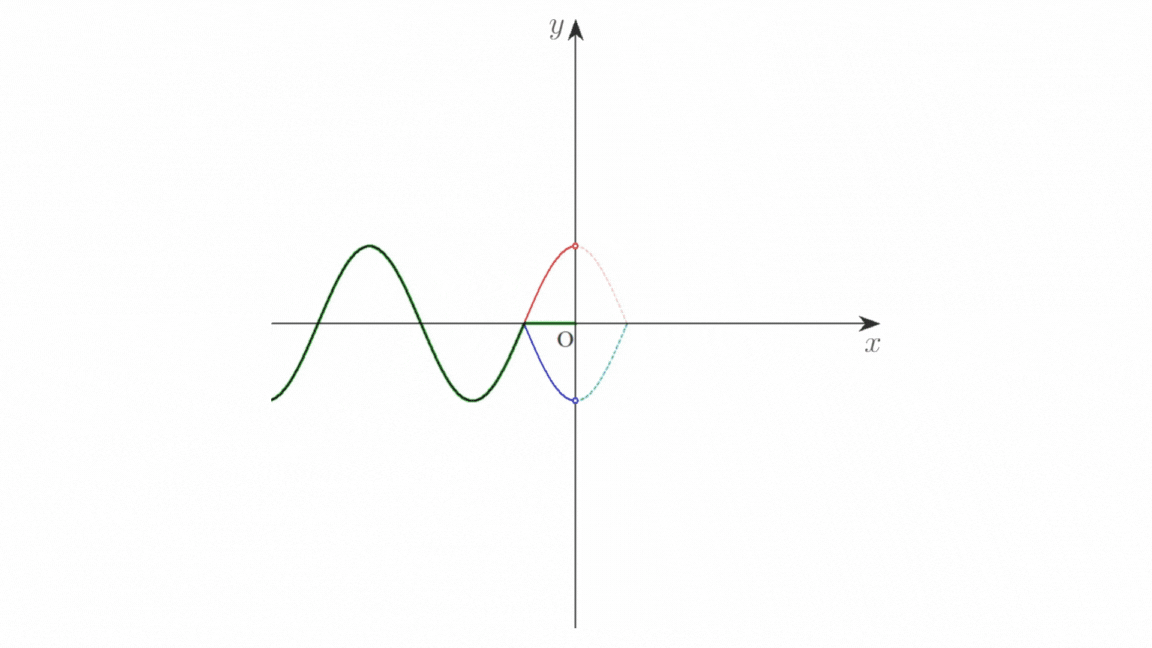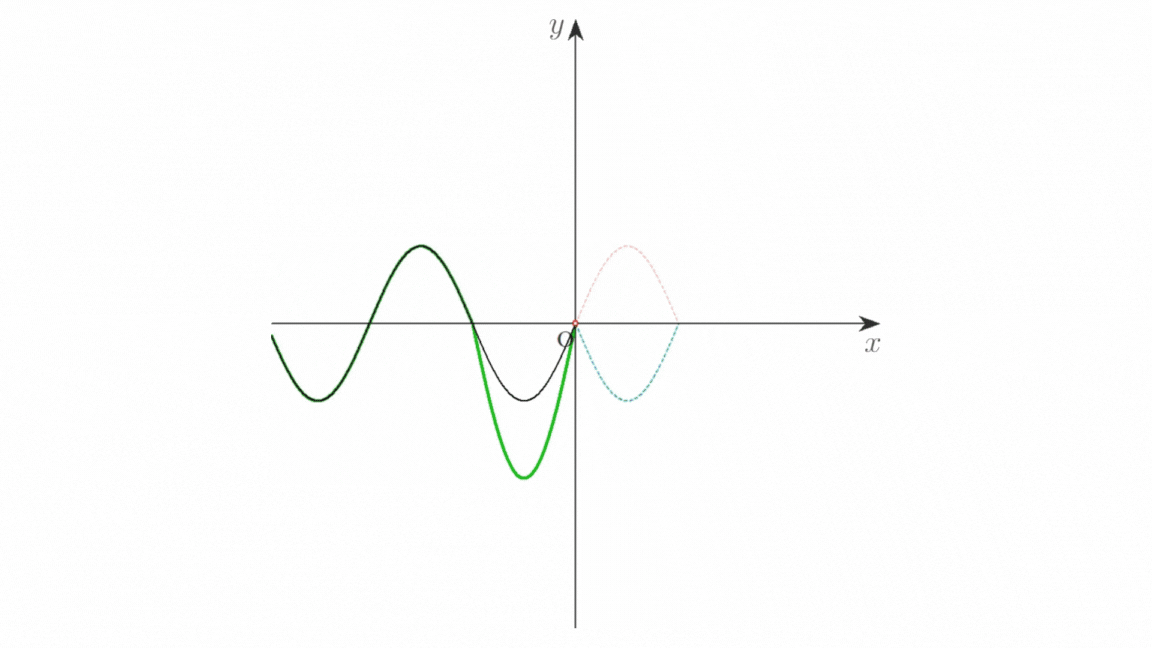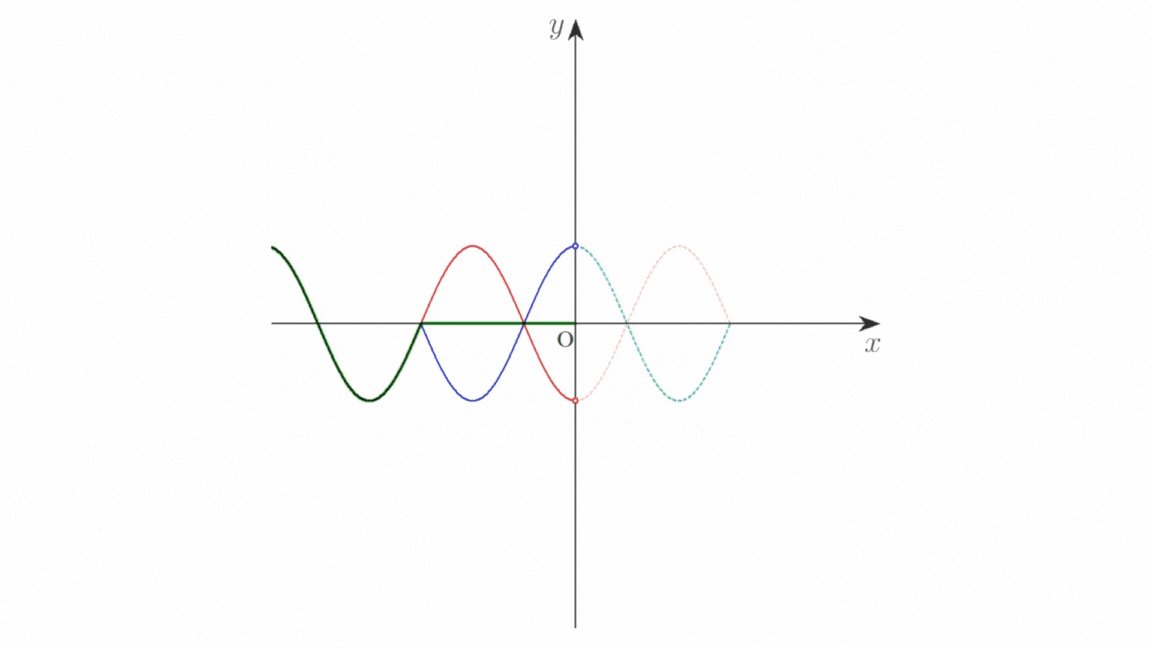
画像 b は,固定端反射の様子を示したものです。入射波を赤色の実線,反射波を青色の実線,これらの合成波を緑色の実線で表しています。
媒質の端 \(\mathrm{O}\) が固定端のとき,端の変位は常に \(0\) なので,端における入射波による振動と反射波による振動は逆位相です。
画像 b(クリックで拡大)
\(\mathrm{O}\) の入射波による振動を○,反射波による振動を○で表しました。
もし \(\mathrm{O}\) が媒質の端でないならば,入射波,反射波による振動が \(x\) 軸の正の向きに伝わり,それぞれ赤色の破線,青色の破線で示した波が生じるはずです。2 つの破線は \(x\) に関して対称となっています。
青色の破線の波がはね返るので,反射波の波形は,赤色の破線を \(x\) に関して折り返し,さらに \(y\) 軸に関して折り返したものとなります。


