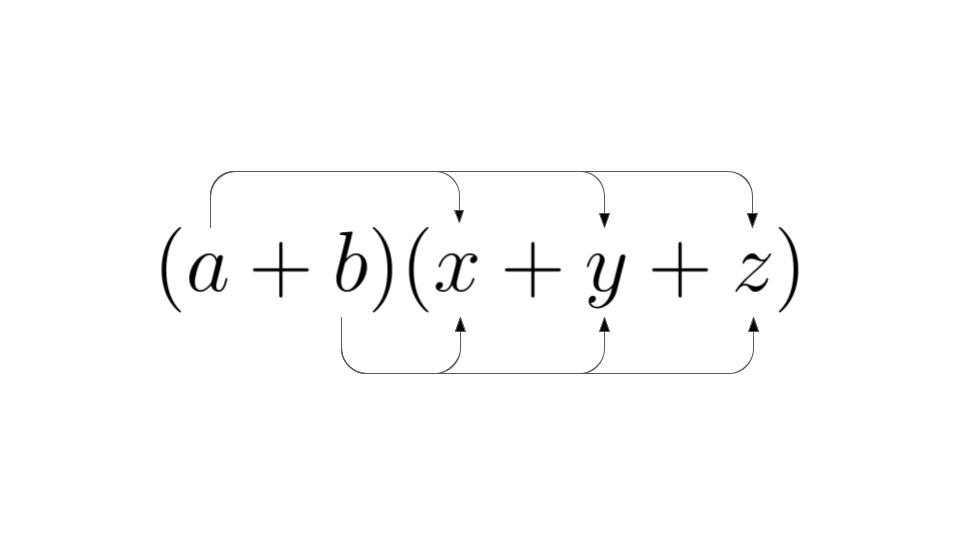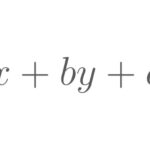いくつかの多項式の和・差・積の形で表された式は,交換法則,結合法則,分配法則を繰り返し用いることで\(\,\)1\(\,\)つの多項式に変形することができます。
1.数と多項式の積
多項式どうしの計算の前に,数と多項式の乗法に触れておきます。
⑴
⑵
⑶
分配法則を意識して計算過程を書いています。
⑴
\(3(x-2)=3\{x+(-2)\}\,\)ですから,\(\,A=3\),\(B=x\),\(C=-2\,\)として分配法則\(\,A(B+C)=AB+AC\,\)を適用すれば計算できます。
⑵
括弧内の多項式の項が\(\,\)3\(\,\)つになっていますが,\(A=2\),\(B=x^2-3x\),\(C=6\,\)とおけば,分配法則を適用できることがわかります。\(\,\)2\(\,\)行目から\(\,\)3\(\,\)行目で再び分配法則を用いて括弧を外しています。
⑶
⑵\(\,\)からわかるように,分配法則を繰り返し用いれば,括弧内が\(\,\)3\(\,\)つ以上の項からなる多項式の場合でも,括弧外の数とカッコ内のそれぞれの項とを掛け合わせればよいことがわかります。
解答にもあるように
ですから,括弧を外すと各項の符号が入れ替わります。
例\(\,\)1\(\,\)では非常に丁寧に計算過程を書きましたが,慣れてくれば頭のなかで計算し,問題の式からいきなり最終行の式を書けるはずです。
2.加法と減法
加法と減法は,同類項をまとめる要領で計算できます。
\[\begin{align}
&A=2x^2-4xy\\\\
&B=-3xy+y^2-2\\\\
&C=x^2+4y^2+1
\end{align}\] とする。次の計算をせよ。
⑴
⑶
⑸
⑹
\(A+B\)
\(A-B+2C\)
\(2A-2(A+C)-3(2B-A)\)
\(3(A-C)-2\{2A-(B-C)\}\)
⑵
⑷
\(2A-C\)
\(-A+3B-C\)
解答
⑵,⑶,⑷,⑹\(\,\)は答えのみ載せます。
⑴
⑵
⑶
⑷
⑸
⑹
⑴~⑷\(\,\)は多項式を代入して計算するだけです。
⑸,⑹\(\,\)については,そのまま代入しても同じ結果が得られるのですが,問題の式は\(\,\)3\(\,\)つの文字\(\,A\),\(B\),\(C\,\)の多項式ですから,まずこれを整理して簡単な形にしてから代入した方が計算がらくです。
3.乗法
a.指数法則
多項式の乗法は,次の指数法則を用いて計算します。
\(m\),\(n\,\)を正の整数とする。
1
2
3
\({(a^m)}^n=a^{mn}\)
\({(ab)}^n=a^nb^n\)
\({(a^4)}^2=a^4 \times a^4=a^{4+4}=a^{4 \times 2}=a^8\)
\({(ab)}^2=ab \times ab=aa \times bb=a^2b^2\)
次の計算をせよ。
⑴
⑶
⑸
\(x^3 \times x^4\)
\({(xy)}^3\)
\({(x^2)}^2 \times {(x^3)}^4\)
⑵
⑷
⑹
\({(x^3)}^4\)
\(x^2 \times x^3 \times x^4\)
\({(xyz)}^4\)
解答
⑷~⑹\(\,\)では指数法則を繰り返し用いています。これらの計算も,慣れてくれば途中の式を書くことなく答えを出せるはずです。
指数法則の\(\,\)1\(\,\)と\(\,\)2\(\,\)を混同しないように注意が必要です。
⑴
⑵
⑶
\({(x^3)}^4=x^{3 \times 4}=x^{12}\)
\({(xy)}^3=x^3y^3\)
⑷
⑸
⑹
\({(x^2)}^2 \times {(x^3)}^4=x^{2 \times 2} \times x^{3 \times 4}=x^4 \times x^{12}=x^{4+12}=x^{16}\)
\({(xyz)}^4={\{(xy)z\}}^4={(xy)}^4z^4=x^4y^4z^4\)
b.式の展開
いくつかの多項式の積の形で表された式は,分配法則を用いて\(\,\)1\(\,\)つの多項式に変形することができます。このような変形をすることを式を展開するといいます。
分配法則\(\,(A+B)C=AC+BC\,\)において
とおくと
上の例では\(\,x^2-x+3\,\)を\(\,\)1\(\,\)つのかたまりと捉えて計算しましたが,\(2x-1\,\)を\(\,\)1\(\,\)つのかたまりと捉えても同じ結果が得られます。
次の式を展開せよ。
⑴
⑶
⑸
\((y+1)(x+2y-3)\)
\((x-2y+1)(3x+y-2)\)
⑵
⑷
\((a^2+1)(a^2-2a+2)\)
解答
答えのみ示します。
⑴
⑵
⑶
⑷
⑸
\(x^2-4x+3\)
\(xy+2y^2+x-y-3\)
\(a^4-2a^3+3a^2-2a+2\)
\(3x^2-5xy-2y^2+x+5y-2\)
3.練習問題
次の式を計算をせよ。
⑴
⑵
⑶
⑷
⑸
⑹
⑺
⑻
⑼
⑽
⑾
⑿
\((3x^2-xy+2y^2)-(x^2+2xy-5y^2)\)
\((x^3-3x+5)-2(x^2-3+6x)\)
\(2(x^2-2x+2)-(x^2+6x-3)-3(2x^2+4x-1)\)
\((2x-3)(x^2+4x-2)\)
\((3x-2)(2x-5)\)
\((a^2-ab+b^2)(2a^2+ab-4b^2)\)
\((x^2+2)(x-1)+3(x-2)(x^2-2)\)
\((2a-b)(b+c)-2(b-3c)(c+2a)+2(2c+3a)(a-2b)\)
\((x-1)(x^3+x^2+x+1)\)
\((x+2)(3x-1)(2x^2+x-5)\)
\((x-y-1)(x+4y+3)(3x-4y+5)\)
解答
⑴~⑽\(\,\)については答えだけを示します。
⑴
⑵
⑶
⑷
⑸
⑹
⑺
⑻
⑼
⑽
\(2x^2-3xy+7y^2\)
\(x^3-2x^2-15x+11\)
\(-5x^2-22x+10\)
\(2x^3+5x^2-16x-6\)
\(6x^2-19x+10\)
\(2a^4-a^3b-3a^2b^2+5ab^3-4b^4\)
\(4x^3-7x^2-4x+10\)
\(6a^2-b^2+6c^2-14ab-11bc+18ca\)
\(x^4-1\)
⑾\(\,\)は\(\,\)3\(\,\)つの多項式の積ですが,一度に展開するのは難しいので,まずは最初の\(\,\)2\(\,\)つの積を計算します。
⑾
⑿\(\,\)はさらに複雑です。そのまま展開していくと大変なことになりそうなので,1\(\,\)つの文字(解答では\(\,x\))に着目して計算していきます。計算過程をすべて書いていると長くなってしまうので,一部省略しています。
⑿