領域とは
1.定義と簡単な例
変数 \(x,\,y\) についての不等式を満たす座標平明上の点 \(x,\,y\) 全体の集合を,その不等式の表す領域といいます。
いくつかの例を見てみましょう。
例 1 不等式 \(y>-x+1\;\cdots\cdots\;①\) の表す領域
例えば,直線 \(x=\sqrt{2}\) 上の点 \((\sqrt{2},\,y_1)\) が①の表す領域にあるとすると,\(y_1>-\sqrt{2}+1\) が成り立つので,点 \((\sqrt{2},\,y_1)\) は \(x\) 軸に垂直な直線 \(x=\sqrt{2}\) の \(y>-\sqrt{2}+1\) の部分の上 (図 1-1)にあります。逆に,この図形上の点はすべて①を満たします。
すべての実数 \(x\) について同様に考えると,①の表す領域は図 1-2 の斜線部分です。ただし,境界線である直線 \(y=-x+1\) は領域に含みません。
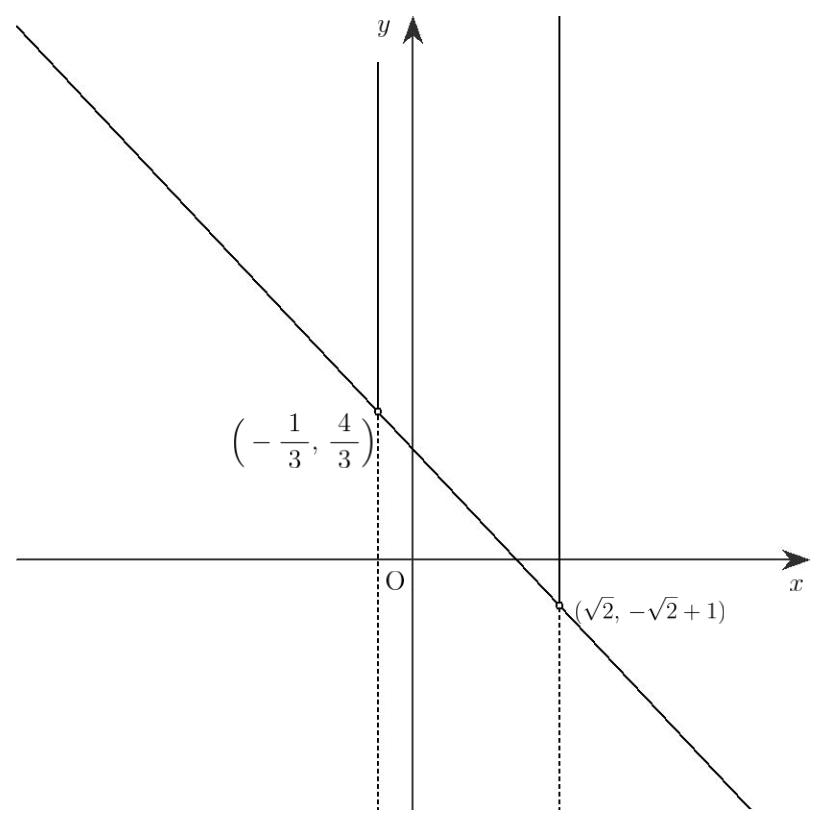
(図 1-1)
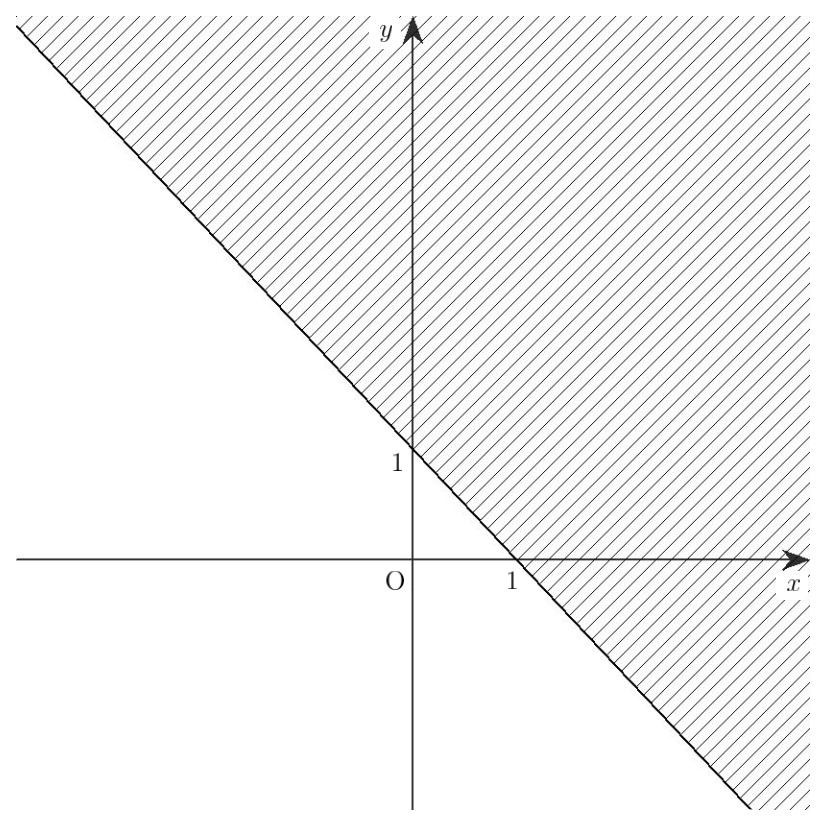
(図 1-2)
例 2 不等式 \(y\le x^2\;\cdots\cdots\;②\) の表す領域
同じように考えてみましょう。
点 \((x_1,\,y_1)\) が②の表す領域にあるとは,\(y_1\le {x_1}^2\) が成り立つことです。よって,点 \((x_1,\,y_1)\) は直線 \(x=x_1\) 上にあって,\(y\) 座標が \({x_1}^2\) 以下です。
一方で,点 \((x_1,\,{x_1}^2)\) は放物線 \(y=x^2\) 上にあります。
したがって,②の表す領域は,放物線 \(y=x^2\) とその下側の部分であり,図示すると図 1-3 の斜線部分(境界線を含む)となります。
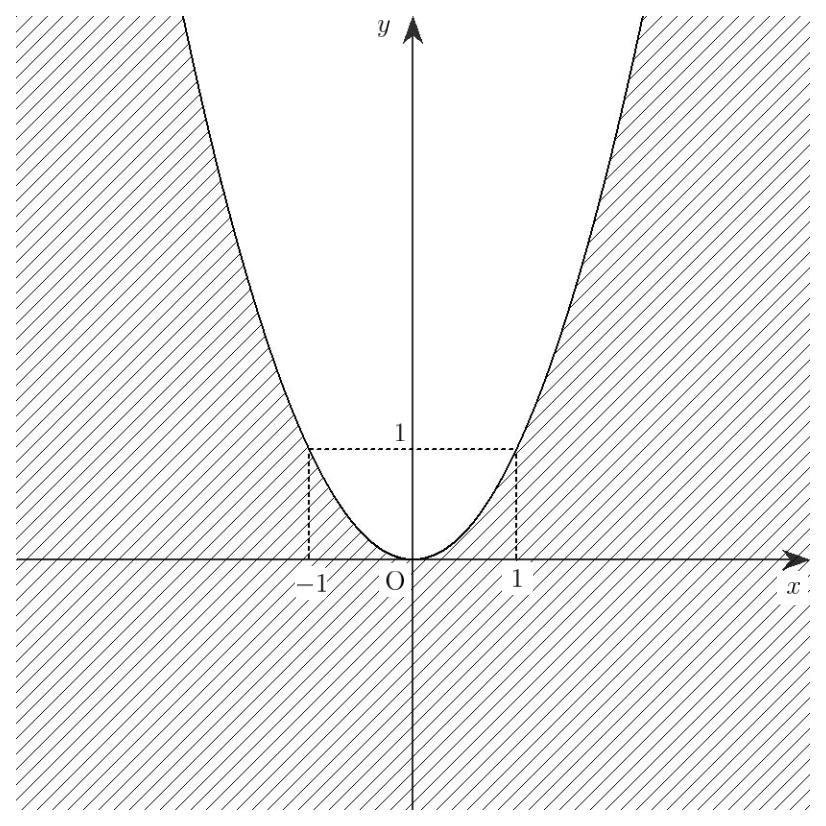
(図 1-3)
例 3 不等式 \(x^2+y^2<1\;\cdots\cdots\;③\) の表す領域
点 \((x_1,\,y_1)\) が③の表す領域にあるとは,\({x_1}^2+{y_1}^2<1\) が成り立つことです。これは 2 点 \((0,\,0)\),\((x_1,\,y_1)\) の距離が 1 より小さい,すなわち点 \((x_1,\,y_1)\) が円 \(x^2+y^2=1\) の内部にあることを表しています。
よって,③の表す領域は円 \(x^2+y^2=1\) の内部であり,図 1-4 の斜線部分(境界線を含まない)です。
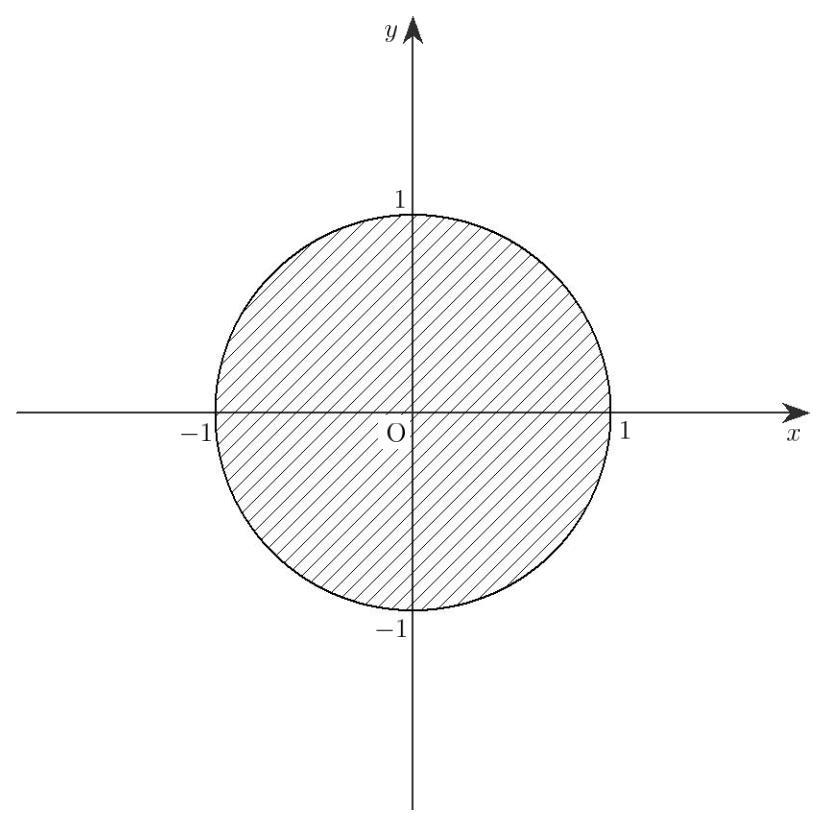
(図 1-4)
2.連立不等式の表す領域
連立不等式の表す領域は,連立された個々の不等式の表す領域の共通部分です。
例題 1
次の連立不等式の表す領域を図示せよ。
(1) \(x+4y\le 7,\quad 3x+y\ge -1,\quad 5x+2y\ge -3\)
(2) \(x+y\ge 1,\quad x^2+y^2\le 2\)
領域と最大・最小
領域分野の代表的な問題として,実数 \(x,\,y\) がいくつかの不等式を満たすとき,\(f(x,\,y)\) の最大値・最小値を求める問題が挙げられます。
とくに,条件の不等式がすべて 1 次不等式のときの \(x,\,y\) の 1 次式の最大値・最小値を求める方法を,線形計画法といいます。ここでは,線形計画法の問題を用いて,領域に関する最大・最小問題を取り上げます。
1.例題とその解答
例題 2
実数 \(x,\,y\) が 4 つの不等式\[x\ge 0,\quad y\ge 0,\quad 2x+y\le 8,\quad x+3y\ge 9\;\cdots\cdots\;(*)\]を満たすとき,\(x+2y\) の最大値を求めよ。
解答
点 \((x,\,y)\) が存在する領域を \(D\) とすると,領域 \(D\) は 4 点 \((0,\,0),\;(4,\,0),\;(3,\,2),\;(0,\,3)\) を頂点とする四角形の周および内部である。
(☆)\(x+2y=k\;\cdots\cdots\;④\) とおくと,④は傾きが \(\displaystyle -\frac{\;1\;}{2}\) で \(y\) 切片が \(\displaystyle \frac{\;k\;}{2}\) の直線を表す。
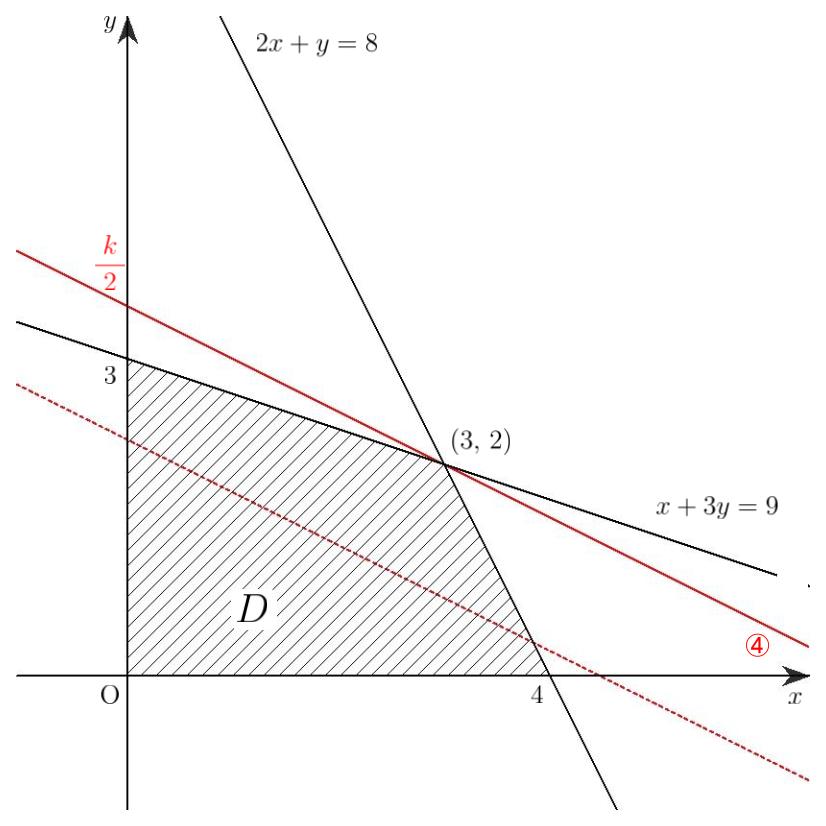
(図 2-1)
(★)求める最大値は,直線④が領域 \(D\) と共有点をもつような \(k\) の最大値である。
境界線 \(2x+y=8,\quad x+3y=9\) の傾きはそれぞれ \(\displaystyle -2,\; -\frac{\;1\;}{3}\) であり,\(\displaystyle -2<-\frac{\;1\;}{2}<-\frac{\;1\;}{3}\) であるから,\(k\) は直線④が点 \((3,\,2)\) を通るとき最大となり,このとき \(k=3+2\cdot 2=7\)
よって,\(x+2y\) は \({x=3,\,y=2}\) のとき最大値 \(7\) をとる。
2.考え方
点 \((x,\,y)\) が動く範囲,すなわち領域 \(D\) を座標平面上に図示することは,特に難しいことではないと思います。4 つの不等式が表す領域の共通部分に斜線を引けばいいだけです。
立ち止まる箇所があるとすれば,それは☆印,★印を付した行でしょう。どうして \(x+2y=k\) とおくのか,どうして直線 \(x+2y=k\) が領域 \(D\) と共有点をもつような \(k\) の最大値を考えればよいのか,ということです。
連立方程式 \((*)\) を満たす実数の組 \((x,\,y)\) を 1 つとってくると,それに対して \(x+2y\) の値がただ 1 つに決まります。例えば
\(x=1,\;y=2\) のとき \(x+2y=1+2\cdot 2=5\)
\(\displaystyle x=\frac{\;5\;}{2},\;y=\frac{\;1\;}{3}\) のとき \(\displaystyle x+2y=\frac{\;5\;}{2}+2\cdot \frac{\;1\;}{3}=\frac{19}{\;6\;}\)
です。このように,1 つ 1 つの \((x,\,y)\) について \(x+2y\) を計算し,最大値を求められればよいのですが,\((*)\) を満たす \((x,\,y)\) は無数に存在するので,そんなことは不可能です。
そこで,見方を変えます。
問題になっているのは \(x+2y\) のとりうる値のうち最大のものですから,\(x+2y\) の値を 1 つ決めて,それを \(k\) とおくと,問題は
\(x+2y=k\) となる実数の組 \((x,\,y)\) で,\((*)\) を満たすものが存在するような \(k\) の最大値を求めよ。
と言い換えることができます。これを図形的に解釈すると
直線 \(x+2y=k\) 上の点 \((x,\,y)\) で,領域 \(D\) に含まれるものが存在するような \(k\) の最大値を求めよ。
となります。よって,直線 \(x+2y=k\) と領域 \(D\) が共有点をもつような \(k\) の最大値を求めればよい,ということです。
\(k\) の値が変化すると,直線④は,傾きは変わらず \(y\) 切片だけが変わります。\(k\) が最大になるときと\(\displaystyle \frac{\;k\;}{2}\) が最大になるときとは一致しますから,領域 \(D\) の境界線の傾きも考慮すると,図 2-1 から,直線④が点 \((3,\,2)\) を通るとき \(k\) は最大となることがわかります。
なお,最小値は \(0\) (\(x=0,\;y=0\) のとき) です。
3.おわりに
領域が関係する最大・最小問題は,条件の不等式が 1 次不等式だけのものや,1 次式の最大値・最小値を求めるものに限りません。
しかし,基本となる考え方は同じです。条件に 2 次不等式が登場することがあっても,慌てることはないでしょう。

